
| RUS ENG |
| Full version |

|
|
| SEMINARS |
|
Mathematics of Artificial Intelligence
|
|||
|
|
|||
|
Slow transients and bifurcation of attractors A. N. Gorban' University of Leicester |
|||
|
Abstract: The behavior of dynamical systems in the limit (as time approaches infinity) has been extensively studied, whereas the transition processes and associated singularities remain less understood. In the talk, we systematically analyze how relaxation times, which depend on initial conditions, system parameters, and accuracy, exhibit singularities and how these singularities relate to bifurcations of limit sets. A comprehensive qualitative theory of singularities in transition processes within dynamical systems is presented, focusing on critical delays. The research has practical implications for various fields, including chemistry and physics, where understanding slow relaxation processes is crucial. For instance, in catalytic reactions, interpreting anomalously long transition times is essential for both theoretical understanding and practical applications. Some possible applications to machine learning are also discussed. 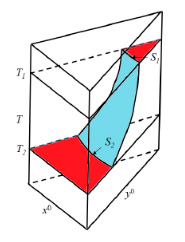
Singularities of relaxation time for catalytic trigger
Language: English |
|||