High-frequency diffraction by a jump of curvature. Tangential incidence

We are concerned with the construction of asymptotic formulas within the framework of systematic boundary layer method [1]. We consider two-dimensional diffraction by the contour $C$ composed of half-line $C_-$ and part of smooth curve $C_+$ (see Fig. 1) with a jump in curvature at the conjugation point $O$. The plane wave $e^{ikx}$ with large wavenumber $k \to \infty$ grazes along $C_-$ to $O$, see Fig. 1. The outgoing wave $u^\mathrm{out}$ is governed by the Helmholtz equation and the Neumann boundary condition:
\begin{equation*} u^\mathrm{out}_{xx}+u^\mathrm{out}_{yy}+k^2u^\mathrm{out}=0, \quad \left. \partial_n \left( u^\mathrm{out} + e^{ikx} \right) \right|_C = 0. \end{equation*}
Here, 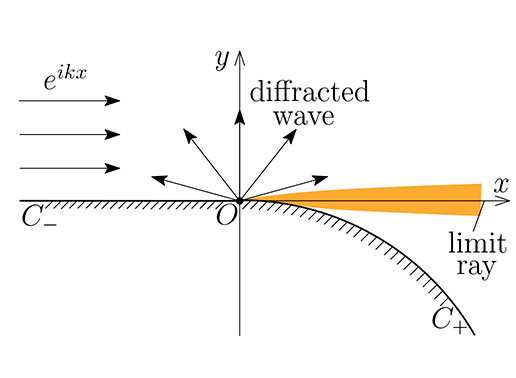$\partial_n$ denotes the derivative along the normal to the contour $C$.

Fig. 1. The geometry of the problem.

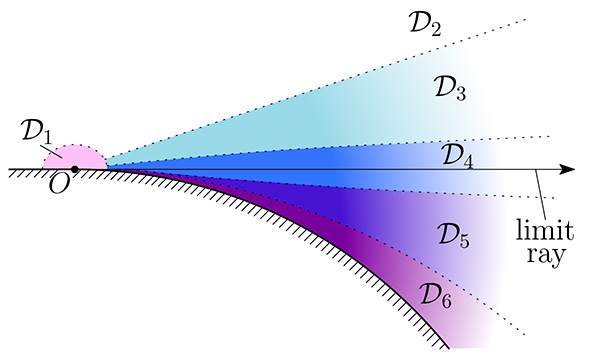
Fig. 2. The sketch of boundary layers.

The problem has been previously addressed by A.V. Popov [2] who, using a heuristic approach, derived an expression for the diffracted cylindrical wave diverging from the jump point $O$ (see Fig. 1).
Our aim is to develop a formal boundary layer approach and construct high-frequency approximations for the wavefield in the neighborhood of the limit ray (orange zone in Fig. 1). We base on the Leontovich—Fock parabolic equation method [1,3]. This allows an asymptotic description of the wavefield in boundary layers surrounding the limit ray (see Fig. 2), which involves novel special functions.
The talk is based on the joined work with A.P. Kiselev [4].