
| RUS ENG |
| Полная версия |

|
|
| ВИДЕОТЕКА |
|
VI Международная конференция «Суперкомпьютерные технологии математического моделирования» (СКТеММ’25)
|
|||
|
|
|||
|
Численное моделирование процессов газовой динамики с применением одной адаптивной искусственной вязкости для полностью консервативных разностных схем Х. Чжан Московский физико-технический институт (государственный университет), г. Долгопрудный, Московская обл. |
|||
|
Аннотация: Уравнения газовой динамики представляют собой выражения основных законов сохранения (массы, импульса и энергии) в сплошной среде. В исследовании и практике полностью консервативные разностные схемы (ПКРС) [1, 2] c адаптивной искусственной вязкостью [3] показывают эффективноть и точность для решения задач газовой динамики. Рассмотрим двухслойную по времени полностью консервативную разностную схему пространственно-одномерного течения сжимаемого газа в переменных Эйлера: \begin{align} \label{eq:eq5} & m_t = -v DIN_D \mu_D^\sim,\\ \label{eq:eq6} & (mu)_t = -v GRAD_\sigma \pi^\sim - v DIT_D(\mu_D^\sim \cdot u_D ^ \sim),\\ \label{eq:eq7} & (m\varepsilon)_t = -\frac{1}{2}\sum_{\Omega(\omega)} (\pi^\sim V DIV_\sigma u^\sim)_\Omega - v DIN_D\mu_{ED}^\sim,\\ \label{eq:eq8} & (m\frac{u^2}{2})_t = - v (u^\sim,GRAD_\sigma \pi^\sim)- v DIN_D(\mu_D^\sim \frac{u^{2\sim}_D}{2}), \end{align} где \begin{align}\nonumber & \mu = \rho u, ~ \mu_E = \varepsilon \mu=Eu, ~ E = \rho \varepsilon, ~ \rho^\sim=\rho^{(\psi_\rho)}, ~ \psi_\rho = const,\\ \nonumber & M_D^\sim = \frac{1}{2}\sum_{\omega(\Omega)}(\rho_\omega u_\omega)^{(0.5)}, ~ \mu_D^\sim = M_D^\sim - \nu_\rho^\sim GRAN_D \rho^\sim,\\ \nonumber & \pi_\Omega^\sim = P_\Omega^{(0.5)}- \nu_u^\sim DIV_\sigma (\rho^\sim u^{(\psi_u)}), ~ P_\Omega = \frac{1}{2}\sum_{\omega(\Omega)}P_\omega, ~ \psi_u = const,\\ \nonumber & M_{ED}^\sim=\frac{1}{2}\sum_{\omega(\Omega)}(E_\omega u_\omega)^{(0.5)}, ~ \mu_{ED}^\sim = M_{ED}^\sim - \nu_E^\sim GRAN_D (\rho^\sim \varepsilon^{(\psi_\varepsilon)}), ~ \psi_\varepsilon = const, \end{align} { В работе [4] предложены методы наполнения АИВ для данной ПКРС .Для тестирования предлагаемых методов проводятся расчёты задач Эйнфельдта [5] и Сода [6]. Часть результатов расчётов представлена в рис. 1 и рис. 2. Результаты показывают высокую точность. Кроме этого численные значения скорости и термодинамических величин (плотность внутренняя энергия и энтропия) совпадают с аналитическими. 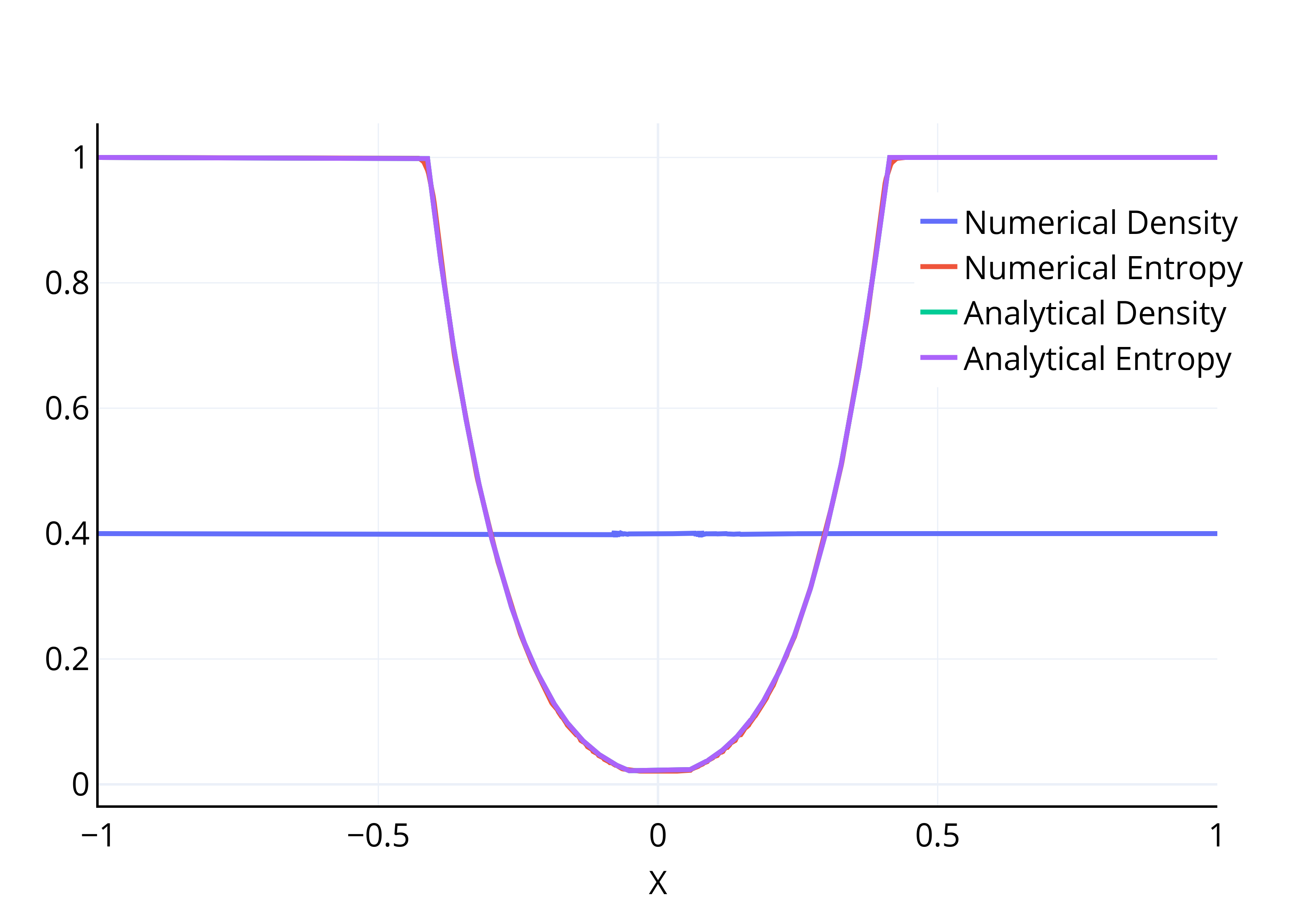
Рис. 1. Профиль плотности и энтропии (
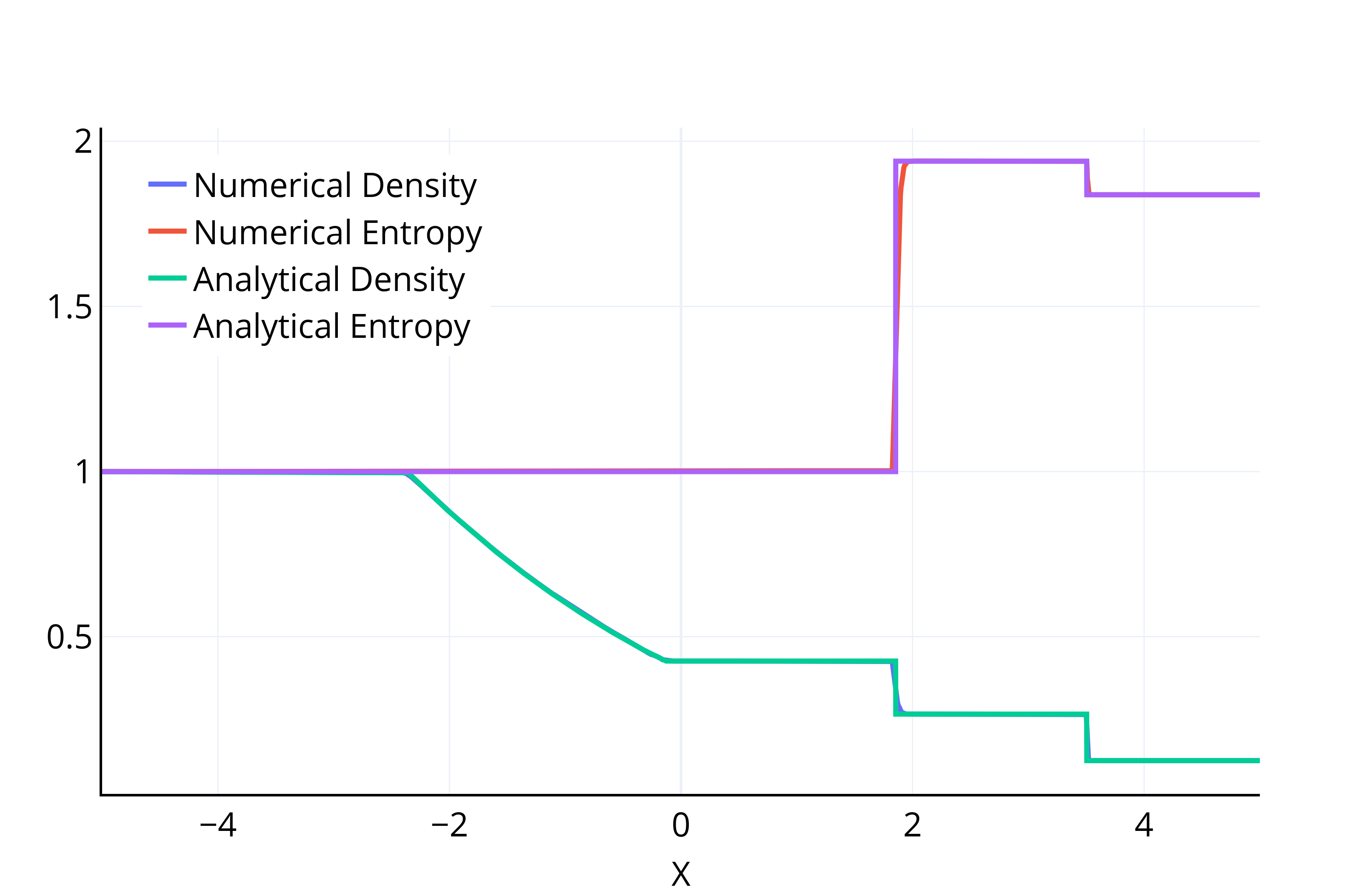
Рис. 2. Профиль плотности и энтропии (
Список литературы
|
|||